example of curvature directions in slam

# Authors: Julien Lefevre <julien.lefevre@univ-amu.fr>

# License: MIT
# sphinx_gallery_thumbnail_number = 2

# importation of slam modules
import slam.generate_parametric_surfaces as sgps
import slam.curvature as scurv

Create quadric mesh

nstep = 20
equilateral = True

K = [1, 0.5]
quadric_mesh = sgps.generate_quadric(
    K,
    nstep=[int(nstep), int(nstep)],
    equilateral=equilateral,
    ax=1,
    ay=1,
    random_sampling=False,
    ratio=0.2,
    random_distribution_type="gaussian",
)

Compute principal directions of curvature

PrincipalCurvatures, PrincipalDir1, PrincipalDir2 \
    = scurv.curvatures_and_derivatives(quadric_mesh)

Calculating vertex normals .... Please wait
Finished calculating vertex normals
Calculating curvature tensors ... Please wait
Finished Calculating curvature tensors
Calculating Principal Components ... Please wait
Finished Calculating principal components

VISUALIZATION USING matplotlib

import numpy as np
import matplotlib.pyplot as plt

Visualization of vector fields with matplotlib

def visualize(mesh, vector_field, colors=None, params=None):
    """
    Visualize a mesh and a vector field over it
    :param mesh: a mesh with n points
    :param vector_field: (n,3) array
    :param colors: (n,3) array
    :param params: params[0] is the length of the quivers
    :return:
    """
    n = mesh.vertices.shape[0]
    if colors is None:
        colors = np.zeros((n, 3))
        colors[:, 0] = 1
    if params is None:
        params = []
        params.append(0.1)

    ax = plt.figure().add_subplot(projection='3d')
    ax.plot_trisurf(
        mesh.vertices[:, 0],
        mesh.vertices[:, 1],
        mesh.vertices[:, 2],
        triangles=mesh.faces,
        shade=True,
    )
    plt.quiver(
        np.array(mesh.vertices[:, 0]),
        np.array(mesh.vertices[:, 1]),
        np.array(mesh.vertices[:, 2]),
        vector_field[:, 0],
        vector_field[:, 1],
        vector_field[:, 2],
        length=params[0],
        colors=colors,
    )

    return ax

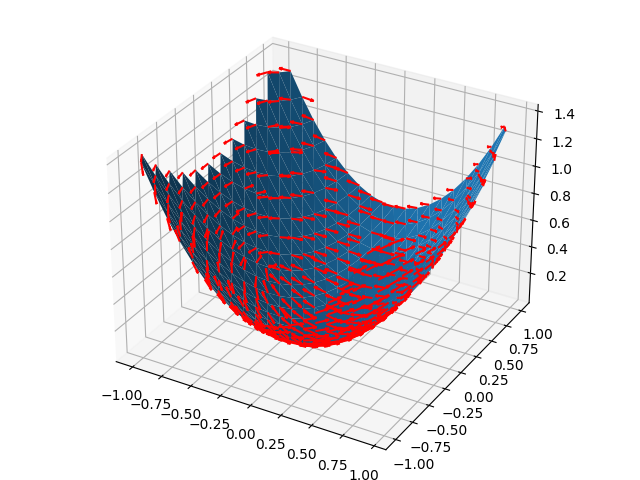
visualize(quadric_mesh, PrincipalDir1)
plt.show()